Probabilités
Si la réalisation d'un événement est soumise au hasard, pour connaître la probabilité de réalisation de cet événement, on doit d'abord définir, à l'aide d'un diagramme, d'un tableau à double entrée ou d'un arbre des choix, l'ensemble des issues possibles.
On peut alors dénombrer celles qui sont favorables à la concrétisation de cet événement.
On peut alors dénombrer celles qui sont favorables à la concrétisation de cet événement.
1. Quel est le vocabulaire des probabilités ?
L'univers des possibles est l'ensemble des issues possibles d'une expérience aléatoire.Les événements élémentaires (ou éventualités) sont les issues possibles de cette expérience. Un événement est une réunion d'événements élémentaires.
La probabilité d'un événement élémentaire est la fréquence supposée de sa réalisation. La probabilité d'un événement est la somme des probabilités de ses événements élémentaires.
Il y a équiprobabilité lorsque les événements élémentaires ont tous la même probabilité de réalisation. Dans ce cas, si a est le nombre d'éléments de l'événement A et n le nombre d'éléments de l'univers :
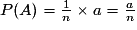 .
.(On divise le nombre de cas favorables par le nombre de cas possibles.)2. Quelles opérations peut-on effectuer sur les événements ?
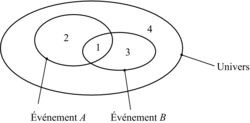
On peut faire l'intersection de deux événements ou leur réunion. On peut aussi définir le complémentaire d'un événement.
- Un élément appartient à l'intersection de deux événements s'il appartient à la fois à l'unet à l'autre.
- Un élément appartient à leur réunion s'il appartient à l'un ou à l'autre, c'est-à-dire à l'un des deux ou aux deux à la fois.
- Un élément appartient au complémentaire d'un événement s'il n'appartient pas à cet événement.
| Événements | Zones concernées | Notation |
|---|---|---|
| A est réalisé | 1 ; 2 | |
| B est réalisé | 1 ; 3 | |
| Uniquement A est réalisé | 2 | |
| Uniquement B est réalisé | 3 | |
| A et B sont réalisés | 1 | 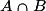 (A inter B) (A inter B) |
| A ou B sont réalisés | 1 ; 2 ; 3 | 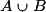 (A union B) (A union B) |
| A n'est pas réalisé | 3 ; 4 | 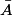 (complémentaire de A) (complémentaire de A) |
| B n'est pas réalisé | 2 ; 4 | 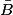 (complémentaire de B) (complémentaire de B) |
| Soit A, soit B est réalisé | 2 ; 3 |
On retiendra l'égalité fondamentale :
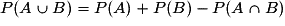 .
.
Si l'intersection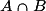 ne comporte aucun élément, on dit alors que les événements A et B sont disjoints. On écrit alors :
ne comporte aucun élément, on dit alors que les événements A et B sont disjoints. On écrit alors :
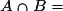
 (ensemble vide).
(ensemble vide).
Dans ce cas alors :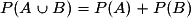 .3. Quelle est la différence entre les notations
.3. Quelle est la différence entre les notations 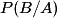 et
et 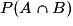 ?
?
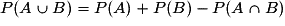 .
.Si l'intersection
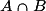 ne comporte aucun élément, on dit alors que les événements A et B sont disjoints. On écrit alors :
ne comporte aucun élément, on dit alors que les événements A et B sont disjoints. On écrit alors :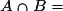
 (ensemble vide).
(ensemble vide).Dans ce cas alors :
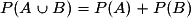 .3. Quelle est la différence entre les notations
.3. Quelle est la différence entre les notations 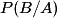 et
et 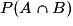 ?
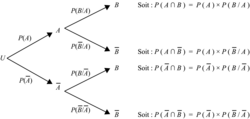
?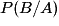 désigne la probabilité que l'événement B soit réalisé, à la condition que l'événement A le soit déjà. C'est une probabilité conditionnelle. On lit « probabilité de B sachant A », et on note aussi
désigne la probabilité que l'événement B soit réalisé, à la condition que l'événement A le soit déjà. C'est une probabilité conditionnelle. On lit « probabilité de B sachant A », et on note aussi 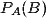 .
.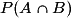 désigne la probabilité que les événements A et B soient réalisés tous les deux à la fois.
désigne la probabilité que les événements A et B soient réalisés tous les deux à la fois.Afin de ne pas confondre ces deux notations, on retiendra l'arbre des probabilités conditionnelles ci-dessous :
On en déduit les formules des probabilités conditionnelles :
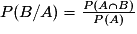 et
et 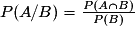 .
.
Par ailleurs :
Les événements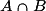 et
et 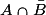 sont disjoints, alors :
sont disjoints, alors :
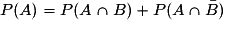 .
.
Les événements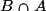 et
et 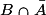 sont disjoints, alors :
sont disjoints, alors :
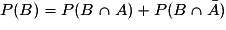 .
.
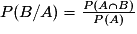 et
et 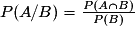 .
.Par ailleurs :
Les événements
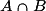 et
et 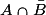 sont disjoints, alors :
sont disjoints, alors :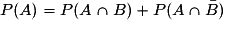 .
.Les événements
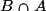 et
et 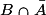 sont disjoints, alors :
sont disjoints, alors :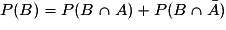 .
.4. Quand dit-on que deux événements sont indépendants ?
Deux événements A et B sont indépendants lorsque la réalisation de l'un ne modifie pas la probabilité de réalisation de l'autre.Plus directement, deux événements A et B sont indépendants lorsque :
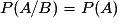 et
et 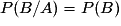 .
.Ce qui équivaut à écrire :
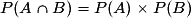 .
.5. Qu'est-ce que l'espérance d'une variable aléatoire ?
Si on associe un nombre réel à chacune des issues d'une expérience aléatoire, cet ensemble de nombres constitue une variable aléatoire. Par exemple, on peut associer à chaque carte d'un jeu de 32 cartes, un nombre de points et chercher ensuite quelles sont les différentes valeurs possibles pour une main de cinq cartes.À une variable aléatoire X de valeurs xi, 1
 i
i  n, on associe la loi de probabilité :
n, on associe la loi de probabilité :| Valeurs de la variable aléatoire | x1 | x2 | … | xi | … | xn | Total |
|---|---|---|---|---|---|---|---|
| Probabilités | p1 | p2 | … | pi | … | pn | 1 |
L'espérance mathématique de X est la valeur moyenne que l'on peut espérer si on renouvelle un grand nombre de fois l'expérience.
On note :
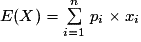 .
.La variance s'écrit :
![V(X)=\sum\limits_{i=1}^n\,p_{i}\times[x_{i}-E(X)]^{2}](http://static1.assistancescolaire.com/t/images/tsti_mat_08_m27.png) ou
ou ![V(X)=\sum\limits_{i=1}^n\,p_{i}\times{x_{i}^{2}}-[E(X)]^{2}](http://static1.assistancescolaire.com/t/images/tsti_mat_08_m28.png) .
.L'écart type s'écrit :
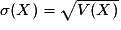 .
.À retenir
Dans une situation d'équiprobabilité, la probabilité P de réalisation d'un événement est donnée par la formule :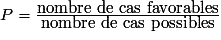 .
.On retiendra les notations :
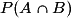 désigne la probabilité de réalisation simultanée des événements A et B ;
désigne la probabilité de réalisation simultanée des événements A et B ;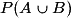 désigne la probabilité que A ou B soit réalisé ;
désigne la probabilité que A ou B soit réalisé ;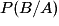 désigne la probabilité de réalisation de l'événement B, sachant que l'événement A l'a été.
désigne la probabilité de réalisation de l'événement B, sachant que l'événement A l'a été.On retiendra les égalités :
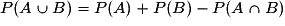
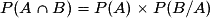
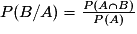 .
.Une variable aléatoire est un ensemble de nombres réels associés à chacune des issues possibles d'une expérience aléatoire.
Pour une variable aléatoire X on a :
- espérance mathématique :
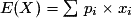 ;
; - variance :
![V(X)=\sum\,p_{i}\times[x_{i}-E(X)]^{2}](http://static1.assistancescolaire.com/t/images/tsti_mat_08_m38.png) ou
ou ![V(X)=\sum\,p_{i}\times{x_{i}^{2}}-[E(X)]^{2}](http://static1.assistancescolaire.com/t/images/tsti_mat_08_m39.png) ;
; - écart-type :
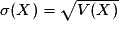 .
.