Les Série
En mathématiques, la série constitue une généralisation de la notion de somme pour une succession infinie de termes. L'étude des séries consiste à évaluer la somme d'un nombre fini n de termes successifs, puis, par un calcul de limite, à identifier le comportement lorsque n devient indéfiniment grand. Un certain nombre de méthodes permettent de déterminer la nature (convergence ou non) des séries sans réaliser explicitement les calculs.
Séries numériques
Une série de terme général  est formellement le couple formé par les deux suites
est formellement le couple formé par les deux suites  et
et 
 est formellement le couple formé par les deux suites
est formellement le couple formé par les deux suites  et
et 
- où, pour tout entier naturel n,
 .
.
Cette suite  est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné,
est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné,  fait correspondre la somme des n + 1 premiers termes de
fait correspondre la somme des n + 1 premiers termes de  .
.
 est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné,
est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné,  fait correspondre la somme des n + 1 premiers termes de
fait correspondre la somme des n + 1 premiers termes de  .
.
Ainsi, la suite des sommes partielles associée à la série de terme général  est de la forme :
est de la forme :
 est de la forme :
est de la forme :
Les séries numériques sont les séries dont les termes xn sont des nombres réels ou des nombres complexes. Il existe également des séries vectorielles, dont les termes sont des vecteurs d'un certain espace vectoriel. On peut ainsi étudier par exemple des séries de matrices ou des séries de fonctions. Leurs spécificités seront indiquées plus bas.
On note la série de terme général xn :  ou
ou  .
.
 ou
ou  .
.Convergent
La série numérique  est dite convergente si la suite des sommes partielles
est dite convergente si la suite des sommes partielles  est convergente ; sa limite S est alors appelée somme de la série, elle est notée
est convergente ; sa limite S est alors appelée somme de la série, elle est notée  , et son calcul est la sommation de la série. Dans le cas contraire, la série est ditedivergente.
, et son calcul est la sommation de la série. Dans le cas contraire, la série est ditedivergente.
 est dite convergente si la suite des sommes partielles
est dite convergente si la suite des sommes partielles  est convergente ; sa limite S est alors appelée somme de la série, elle est notée
est convergente ; sa limite S est alors appelée somme de la série, elle est notée  , et son calcul est la sommation de la série. Dans le cas contraire, la série est ditedivergente.
, et son calcul est la sommation de la série. Dans le cas contraire, la série est ditedivergente.
Deux séries sont dites de même nature si elles sont toutes deux convergentes ou toutes deux divergentes.
On parle de série absolument convergente si la série de terme général |xk| est elle-même convergente (|x| signifiant ici « valeur absoluede x » si x est un nombre réel, « module de x » si x est un nombre complexe, norme s'il s'agit d'un autre élément). Si la série est convergente sans être absolument convergente, on parle de série semi-convergente.
Le fait qu'une série puisse être convergente résout beaucoup de problèmes, comme certains des paradoxes de Zénon. En revanche, il est rare qu'on sache calculer de façon explicite la somme d'une série. Hormis quelques calculs classiques, la théorie des séries a pour objectif de déterminer la nature d'une série sans calcul de la suite des sommes partielles, et éventuellement de procéder à un calcul approché de la somme.
Si la série converge alors son terme général tend vers zéro. La réciproque est fausse (exemple de la série harmonique dont le terme général tend vers zéro tout en étant divergente). Si une série ne respecte pas cette condition, on dit qu'elle diverge grossièrement.
Exemple de Série
La série de terme général  est convergente et sa somme vaut :
est convergente et sa somme vaut :
 est convergente et sa somme vaut :
est convergente et sa somme vaut :
Il est possible de « visualiser » sa convergence sur la droite réelle : on peut imaginer un segment de longueur 2, que l'on découpe en segments successifs de longueurs 1, 1/2, 1/4, etc. Il y a toujours assez de place pour marquer le segment suivant, parce que la longueur restante est constamment égale à la longueur du segment qui vient d'être marqué. Lorsque nous avons marqué 1/2, il reste un morceau de longueur 1/2 non marqué, ainsi nous pouvons encore certainement marquer le prochain 1/4. Cet argument ne peut en aucune façon servir de démonstration que la somme de toutes les longueurs des segments est égale à 2, mais permet de deviner que cette somme va rester inférieure à 2 et donc que la suite des sommes partielles est croissante et majorée.
Cette série est une série géométrique et on démontre sa convergence en écrivant pour tout entier naturel n, sa somme partielle au rang n :
La suite géométrique  de raison 1/2 est convergente de limite nulle donc
de raison 1/2 est convergente de limite nulle donc
 de raison 1/2 est convergente de limite nulle donc
de raison 1/2 est convergente de limite nulle donc
- Si la série
 est convergente, alors pour tout entier naturel n, la somme
est convergente, alors pour tout entier naturel n, la somme  existe, et
existe, et  . Le terme
. Le terme  s'appelle le reste d'ordre n de la série
s'appelle le reste d'ordre n de la série  .Il est facile, par un procédé itératif, de calculer un terme de la suite des sommes partielles. La relation entre la somme partielle, la somme et le reste s'écrit
.Il est facile, par un procédé itératif, de calculer un terme de la suite des sommes partielles. La relation entre la somme partielle, la somme et le reste s'écrit Ainsi, si on sait borner le reste, la somme partielle peut être vue comme une valeur approchée de la somme, avec une incertitudeconnue.
Ainsi, si on sait borner le reste, la somme partielle peut être vue comme une valeur approchée de la somme, avec une incertitudeconnue.Calculs explicites
Il est rare de pouvoir calculer explicitement tous les termes de la suite des sommes partielles.- Les séries géométriques sont celles dont chaque terme est obtenu en multipliant le terme précédent par un nombre constant (appelé raison). La série de terme général
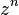 est convergente si et seulement si le nombre (réel ou complexe) z vérifie :
est convergente si et seulement si le nombre (réel ou complexe) z vérifie :  .
.
Exemples : toutes deux convergentes
toutes deux convergentes - Les séries télescopiques sont de la forme
 Elles sont convergentes si et seulement si la suite (bn) converge vers une limite L quand n tend vers l'infini. La valeur de la somme de la série est alors b1 - L.
Elles sont convergentes si et seulement si la suite (bn) converge vers une limite L quand n tend vers l'infini. La valeur de la somme de la série est alors b1 - L.Principe d'études
Il existe un grand nombre de règles pour les séries à termes positifs. Elles sont toutes basées sur le principe de comparaison : si pour tout entier n, on a , alors
, alors- si la série
 converge, la série
converge, la série  aussi ;
aussi ; - si la série
 diverge, la série
diverge, la série  aussi.
aussi.
Pour ces séries à termes positifs, il convient donc de déterminer la nature de certaines séries de références (telles que les séries géométriques), puis de comparer à ces séries.L'étude des séries à termes réels ou complexes, sans hypothèse particulière, peut poser plus de problèmes. Une condition suffisante a une grande importance : si la série des valeurs absolues (série à termes réels) ou des modules (séries à termes complexes) converge, alors la série
converge, alors la série 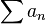 converge également. Elle est alors dite absolument convergente.Il existe des séries convergentes sans être absolument convergentes, comme la série harmonique alternée
converge également. Elle est alors dite absolument convergente.Il existe des séries convergentes sans être absolument convergentes, comme la série harmonique alternée . Les méthodes d'étude pour ce type de série, plus techniques, (critère de convergence des séries alternées, théorème d'Abel, ...)Exemple des Séries
. Les méthodes d'étude pour ce type de série, plus techniques, (critère de convergence des séries alternées, théorème d'Abel, ...)Exemple des Séries- La série harmonique est la série :
 . Cette série est divergente. On montre même que quand
. Cette série est divergente. On montre même que quand  ,
,  où
où  est la constante d'Euler.
est la constante d'Euler. - La série factorielle est la série :
 . Cette série a pour somme
. Cette série a pour somme  , la constante de Néper.
, la constante de Néper. - Les séries de la forme :
 où
où 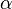 est un réel quelconque,
est un réel quelconque,
sont convergentes si et seulement si . Des séries de ce type sont des séries de Riemann. Elles sont également définies pour
. Des séries de ce type sont des séries de Riemann. Elles sont également définies pour 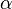 complexe et convergentes si et seulement si
complexe et convergentes si et seulement si  . La fonction zêta de Riemann est la fonction qui, au complexe
. La fonction zêta de Riemann est la fonction qui, au complexe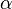 , associe la somme de cette série.
, associe la somme de cette série. - Les séries de la forme :
 , avec
, avec  ,
,
sont convergentes si et seulement si ( ) ou (
) ou ( et
et  ). Ces séries sont les séries de Bertrand.
). Ces séries sont les séries de Bertrand.
Démonstration par intégral du Cauchy
La série de Bertrand a même comportement que l'intégrale en +∞ de la fonction

- Si 1 – α < 0, cette fonction de y est intégrable en +∞ car elle est un O de e–γy pour n'importe quel γ ∈ ]0, α – 1[.
- Si α = 1, elle est intégrable en +∞ si et seulement si β > 1.
- Si 1 – α > 0, elle n'est pas intégrable en +∞ car elle tend vers +∞.
(définie et positive sur ]1,+∞[), sous réserve que f soit décroissante au-delà d'une certaine valeur.Lorsque cette hypothèse de décroissance n'est pas réalisée, c'est-à-dire lorsque α < 0 ou (α = 0 et β < 0), il se trouve qu'on a au contraire croissance à partir d'un certain rang donc la série est trivialement divergente.Lorsqu'elle l'est, c'est-à-dire lorsque (α = 0 et β ≥ 0) ou α > 0, la convergence de la série équivaut à l'intégrabilité en +∞ de la fonction ci-dessus, ou encore, par changement de variable y = ln x, de la fonctionDémonstration plus élémentaire
- Premier cas : α > 1. On pose h = (α – 1)/2, de sorte que quel que soit β, n1+hf(n) = n–h(ln n)–β tend vers 0 lorsque n tend vers l'infini d'où f(n) = o(1/n1+h), ce qui prouve la convergence de la série étudiée.
- Deuxième cas : α < 1. Alors, quel que soit β, 1/(nf(n)) = nα – 1(ln n)β tend vers 0 lorsque n tend vers l'infini d'où 1/n = o(f(n)), ce qui prouve la divergence de la série étudiée.
- Troisième cas : α = 1.
- Premier sous-cas : β ≤ 0. Alors, f(n) ≥ 1/n donc la série diverge.
- Deuxième sous-cas : β > 0. Comme f est ici décroissante, la série étudiée converge si et seulement siadmet une limite finie lorsque a tend vers l'infini. Or, si β ≠ 1, f admet pour primitive x ↦ (ln x)1 – β/(1 – β), qui converge en l'infini si et seulement si β > 1. Enfin, si β = 1, f admet pour primitive x ↦ ln(ln x) qui diverge en l'infini, ce qui termine la démonstration.

- Les séries géométriques sont celles dont chaque terme est obtenu en multipliant le terme précédent par un nombre constant (appelé raison). La série de terme général
Les Vidéo
Reste d'une série convergent











les Vidéo en arab

